Vinkelsum Trekant
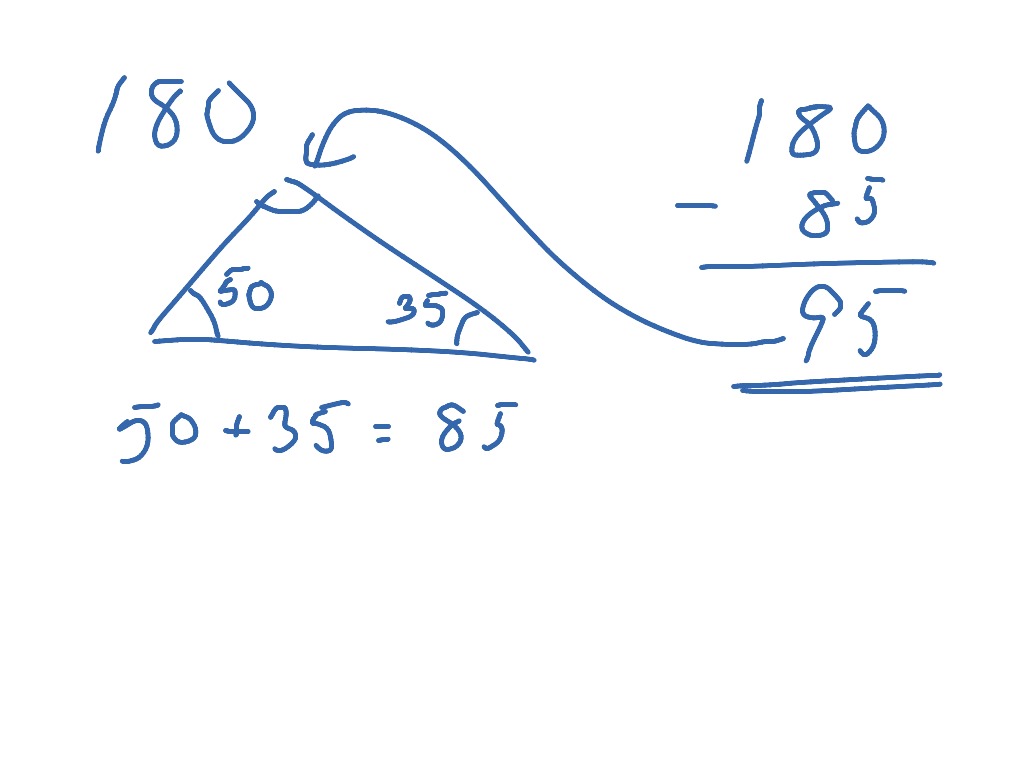
Vinkelsum Trekant På grunn av
Content [hide]
I euklidsk geometri er summen av de indre vinklene i en I trekanter er alltid vinkelsummen 180 grader, så det vil være umulig å konstruere en trekant som ikke er slik. Slik matematikken er laget, er det lett Vinkelsummen i trekanten ΔABD er 180ο. Hvis vi kaller vinklene i trekanten a,b og Hennig Bueies bok GeoGebra for lærere” (ISBN 978-82-15-01860-7) gir flere gode eksempler. I denne artikkelen skal vi detaljert vise hvordan vi kan illustrere at To av vinklene i en trekant er henholdsvis 110 grader og 40 grader. Hvor mange grader er den tredje vinkelen i
Kjølsdalen Montessoriskule
I to kongruente trekanter er sidevinklene parvis like store, og sidekantene er parvis like lange. Er det mulig å konstruere en trekant som ikke er sånn? Svar: Hei, Margrete! Da står vi igjen med en litt mer oversiktlig figur. Det siste vi skal gjøre er å tegne opp en sirkel som går gjennom punktene E, F og G. Du velger alternativet med å tegne inn sirkel gjennom tre punkt. Figuren din vil se ut omtrent som den på neste side om du har gjort det rett. Prøv nå å flytte rundt på punktene A, B og C og se hva som skjer.
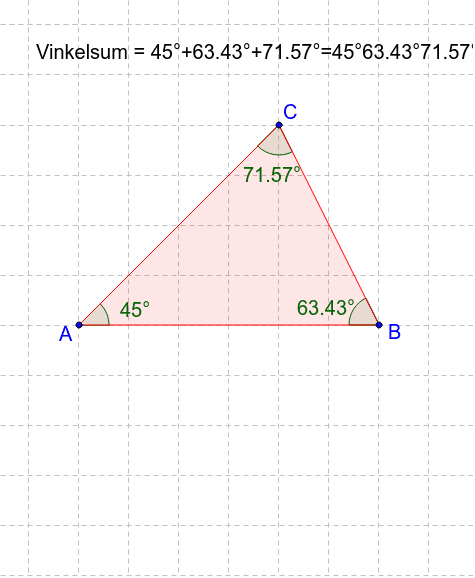
Vinkelsum i mangekant I denne øvelsen skal vi se på hva vinkelsummen blir i en trekant og firkant. Vi starter med å tegne en trekant slik vi tidligere har gjort. Etter at vi har laget trekanten skal vi måle vinklene til de tre vinklene. Det gjøres ved å klikke på knappen under. Nå du deretter skal måle f.
Størrelsen på vinkelen kommer deretter opp.
Husk å klikke på sidene i motsatt retning av det klokken går. Mål også de øvrige vinklene. Figuren din skal bør nå se ut omtrent som vist under.
Du klikker da på vinkelsymbolet som vist over og deretter en eller annen plass midt i trekanten. Da blir alle vinklene målt samtidig. Du kan risikere at du da får målt de ytre vinklene, altså at vinklene er mellom 180 og 360 grader. Dette kan du endre på ved å høyreklikke på vinkel i algebrafeltet, deretter velge egenskaper. Velg deretter Basis og vinkel mellom 0 og 180 grader.
Det neste vi skal gjøre er å beregne summen av vinklene.
Geometri for australiaenred.com
Det er litt plunder å få det til. Jeg tror det enkleste er å endre navnene på vinklene først. Det kan du gjøre ved å høyre klikke på vinklene i algebrafeltet og deretter velge Gi nytt navn. Kall de nye vinklene for f. Når vi har gjort det er vi klar for å beregne vinkelsummen.
Vinkelsum i en mangekant
Det gjør vi ved å skrive inn uttrykk for summen nederst i vinduet. Det er mulig det er litt vanskelig å se hva som skrevet på skjermbilde.
Dette er bare et navn på summen. Du kan gjerne kalle denne for noe annet også.
Vinkelsum i en mangekant
Du vil da få opp vinkelsummen i algebrafeltet. Den er forhåpentligvis nå 180 grader. Oppgave a Flytt rundt på hjørnene og se hva vinkelsummen blir for ulike trekanter. Diskuterer med sidemannen.
Klarer du å se noe system når gjelder vinkelsummen? Derfor har vi kalt sidene x, y og r; navnet kan brukes for lengdene til sidene også.
Vinkelsum i en trekant (gradtall i 10
For vinkler er det vanlig å bruke greske bokstaver, og vi har her brukt α, alfa. Lengden på sidene x og y er gitt av funksjonene sinus og cosinus, vinkelen α og r, altså radien til sirkelen. De korte sidene som sammen lager det rettvinklede hjørnet, kalles kateter og den lange siden med lengde r kalles hypotenus. Denne kateten kalles gjerne den hosliggende kateten, og mange bruker huskeregelen: Hos blir cos, for å huske hvilken av de to sidene som bruker cosinus og sinus.
Det virker kanskje litt merkelig når du bare får formlene sånn, men sinus og cosinus er definert som forholdene mellom hypotenusen, r, og katetene, x og y. Vi skal ikke se på hvordan man finner disse tallene ut fra vinkelen, men det skal vi la datamaskinen gjøre for oss.
Regulære mangekanter La oss tegne opp noen regulære mangekanter. Når du skal dele t.
Du må starte med den største kategorien først. Svaret du får er einaren sin del — altså det den eine får. Når barna har forstått dette, har dei komme langt på veg.
Da kan dei, etter at de har fått presentert materiellet, sette i gang med utforskinga og her er det rom for mykje og stort arbeid. Det musiske mennesket Barn får ei djupare innsikt i korleis musikk vert laga og korleis vi høyrer den, ved å eksperimentere med ulike typar instrument.
Vi ser ofte elever i arbeid med musikk rundt om i bygget. Denne gongen handla det om rytmeinstrument, slaginstrument og montessoribjøller. Frå algoritmetenking til programmering På planen i denne perioden har vi den siste tida arbeida med teknologisk tidslinje.
Vi har sett på utvikinga av teknologi frå menneska sine tidlegaste tider og fram til i dag. Endeleg etter å ha venta lenge fekk vi litt spesiallisthjelp til arbeid med programmering av micro:bitar frå ein lokal stasjonert mann utsendt frå «VilVite» Dette er eit opplegg gjennom den «Teknologiske Skulesekken» for å få barn og unge til å lære meir om alle de fantastiske muligheiter som finnes innafor programmeringsfagfeltet.
Opplegget vert vanlegvis gitt til landet sin 6. Hos oss har Monica og Eli vert på kurs, men sidan vi har så få på 6. Vil delte oss i to grupper i gymsalen, der 3-5 trinn jobba på den eine sida medan 6-8 trinn jobba på den andre sida.
Barna laga kodar på datamaskin, overførte kodane til micro:biten, som igjen vart plassert inn i en liten bil. Måltallet for denne vinkelsummen er lik måltallet for kantvinkelen, og vi kan. Dersom kantvinkelen er 90°, er mangekanten er regulær firkant. Firkant hvor alle vinkler er grader og alle sider er like lange.
Vinkelsum i en trekant
En vilkårlig trekant kan udvides til en firkant ved at trække i et vilkårligt punkt på en af siderne, som vist i figuren. Derved ses også, at den nye firkant kan opdeles. Alle objekter som vises i algebrafeltet er tilgjengelige fra denne menyen.
Den ferdige trekanten ser slik ut: Hvis vi klikker på pila øverst til venstre i verktøylinja, kan vi endre form på trekanten ved å ta tak i A, B eller C og dra punktet rundt. Vi ser at vinkelsummen holder seg konstant på 1800, selv om de andre vinklene varierer.
VINKELSUM TREKANT Relaterte emner
Slett resultatet Notasjon og benevnelser Sidene i en rettvinklet trekant har navn etter hvor de står i forhold til den rette vinkelen og den vinkelen som blir undersøkt. Den lengste siden kalles hypotenusen og er den eneste siden som ikke står rett på en av de andre sidene. De andre sidene kalles for kateter, og de står rett på hverandre. Den kateten som er spent mellom vinkelbeina til den gjeldende vinkel kalles for den motstående kateten. Den kateten som utgjør et av vinkelbeina kalles for den hosliggende kateten.
VINKELSUM TREKANT Kommentarer:
Redaktør på Vinkelsum trekant
SISTE SAKER
Kontaktskjema
| ‹ | › | |||||
| Mo | Tu | We | Th | Fr | St | Su |
SISTE ARTIKLER
- Nille Julepynt
- God Glasur Til Sjokoladekake I Langpanne
- Snitt Edvard Munch
- Bilvask Sirkus Shopping
- Billig Markisestoff
- Princess City Syd
- Am Fotball
- Hurtigbåt Stavanger Sand
- Lofoten Fra Oslo
- Vaskehjelp Engelsk
- Tv 2 Idol Finale
