Cos Tabelle

---

Cos Tabelle Forundret

---

---

I matematikk er tabeller med trigonometriske funksjoner nyttige på en rekke områder. Før eksistensen av lommekalkulatorer, var trigonometriske tabeller viktig for navigasjon, vitenskap og ingeniørfag Bradis tabeller sin, cos, tg, ctg. Trigonometri tabell inneholder de beregnede verdiene for trigonometriske funksjoner i en viss vinkel fra 0 til 360 grader Vi definerer funksjonene cosu, sin u og tan u ved at. cos u = førstekoordinaten til punktet P, De viktigste er sammenfattet i denne tabellen: Play Video Vi kan tegne grafene til de trigonometriske funksjonene på samme måte som vi tegner andre grafer: Ved å sette opp tabell og regne ut så mange funksjonsverdier Den følgende tabellen viser omregningene for noen vanlige vinkler: men parentesene rundt vinkelen er ofte utelatt, f.eks

Hva er forskjellen mellom kostnadsbasert optimalisering Regelbasert optimalisering?

Optimalisering i SQL

Hvordan stiller du inn SQL-spørsmål for å forbedre ytelsen? Det er forskjellige metoder for å stille inn SQL-spørsmål. Mens du stiller inn spørringen, er det ulike faktorer som påvirker ytelsen.

Først og fremst trinnet er å sjekke forklaringsplanen for å forstå den nåværende gjennomføringsbanen og kostnadene ved hvert trinn. Neste trinn er å sjekke om noen underspørsmål eller filtre kan redusere antall rader som returneres av den.

Når disse trinnene er utført, er neste trinn å sjekke hvilken type optimizer som brukes. Hvis det er kostnadsbasert optimaliseringsprogram, samler den statistikken for å evaluere spørringen.

Integrasjonsregler Matematikk

Vi må se om statistikken er oppdatert riktig eller ikke. Hvis ja, så ordne om forholdene tredje regel for regelbasert optimaliseringsprogram.

Sjekk deretter om rekkefølgen på tabellnavn gjør noen forskjell i spørringen og omorganisere dem også. Noen ganger vil det påvirke ytelsen basert på selektiviteten til kolonnene.

Boken ble gjentatte ganger reprinted i sovjetider med store sirkulasjoner opptil 500. Bordfunksjonalitet De vanligste er tabeller som inneholder Trigonometriske funksjoner for eksempel sinus, kosinus, tangent, kotangenes og arctanens.

Bihuler og cosine bord På grunn av den brede bruken av bihuler og cosine i pedagogiske oppgaver, er dette de vanligste parentesene fra bordene.

Trigonometri

Det gir verdien av disse trigonometriske funksjonene for enhver akutt vinkel. Ved hjelp av flere høyttalere kan du finne mer nøyaktige spesifikasjoner. Hvis du trenger enda mer nøyaktige indikatorer, må du bruke korreksjonsfaktorer, og ta og legge dem til nærmeste tabellverdi. Du kan bruke verdiene i høyre kolonne, men mye mer praktisk å beregne hjørnet gjennom Sinus tilskudd til 90 °. Asin-funksjonen returnerer arcsinusen, eller invers sinus, til argumentet.

Arcsinusen er vinkelen hvis sinus er argumentet.

Enhetssirkelen

Atan-funksjonen returnerer arctangensen, eller invers tangens, til argumentet. For å finne verdiene til sinus for en vinkel, må du finne skjæringspunktet mellom raden som inneholder det nødvendige antallet grader i cellen lengst til venstre og kolonnen som inneholder det nødvendige antallet minutter i den øvre cellen.

Hvis den nøyaktige verdien av vinkelen ikke er i Bradis -tabellen, bruker vi hjelp av korreksjoner. Rettelser for ett, to og tre minutter er gitt i kolonnene til høyre i tabellen. For å finne verdien av sinusen til en vinkel som ikke er i tabellen, finner vi verdien nærmest den. Deretter legger du til eller trekker fra korreksjonen som tilsvarer forskjellen mellom vinklene.

Dynamiske laster og utmattingsberegninger Dynamisk belastning kan føre til dannelse og vekst av sprekker. Sprekkene kan over tid bli så store at de fører til et utmattingsbrudd.

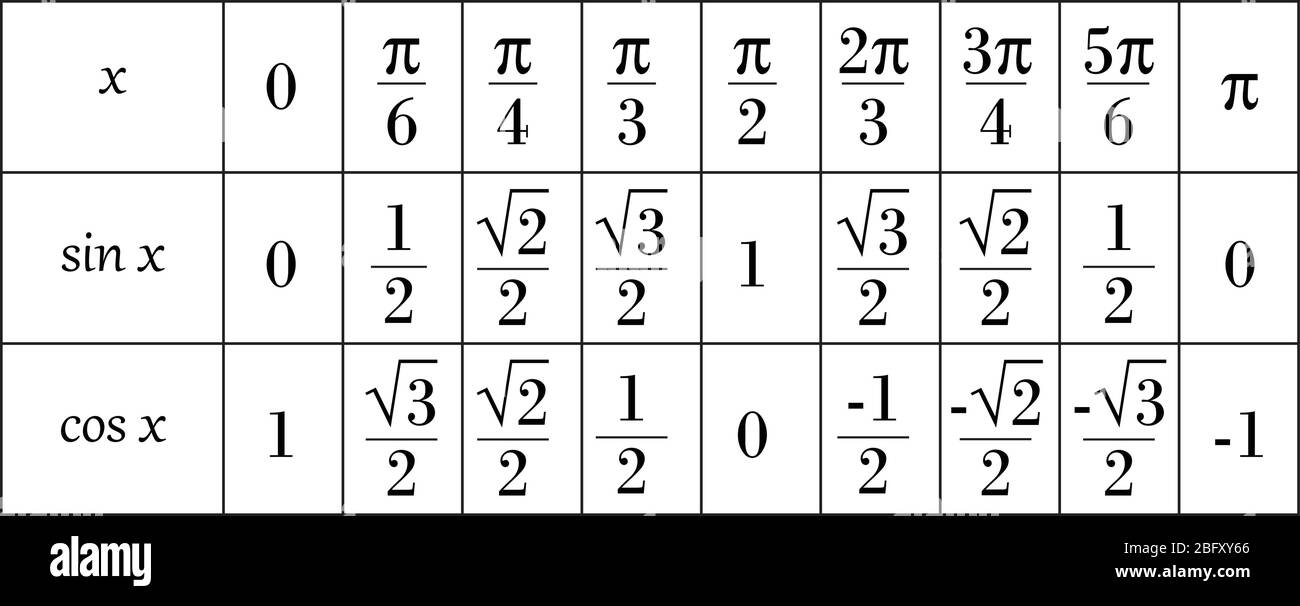
Noen viktige verdier av sin x, cos x og tan x på tabellform Verdiene i tabellen under bør du memorisere. Å kunne disse utenat vil være til stor hjelp i løsingen av trigonometriske ligninger. Men et kvarter før slutt fikk Haslum orden på forsvarsspillet sitt og snudde 24-28 til 30-28.

Fordi du du ganger sammen to enheter. Der har jeg brukt størrelsene, det er en liten, men vesentlig forskjell i denne sammenhengen.

COS TABELLE Relaterte emner

Ver material completo no app Pré-visualização Página 10 de 15 buttsveisen. Ved full gjennomsveising vil den tillatte spenningen i sveiseforbindelsen være den samme som den tillatte spenningen i det svakeste materialet i forbindelsen under forutsetning av at sveiseavsett fra benyttet elektrode ikke har flytspenning eller bruddfasthet som er lavere. De andre delene i løftekurven skal sveises fast med full gjennomsveisede buttsveiser med V-fuge. K-sveisene skal være like sterk som det svakeste materialet i forbindelsen og area. Den jevnførende von Mises spenningen i sveisen og grunnmaterialet i løfteøret er den samme og er beregnet under.